Trees
A tree is a finite set of nodes such
that
1.
there is a specially designated node called root node.
2.
the remaining nodes are partitioned into n>=0 disjoint sets T1, T2,
T3 ---Tn
where each of these sets is a
tree. T1, T2, T3 ---Tn are called sub
trees.
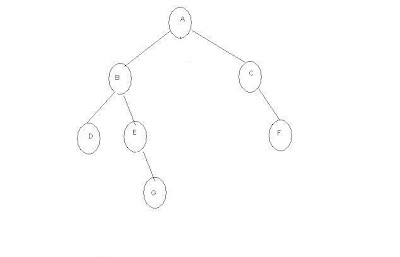
The above tree has 12 nodes. A node is nothing but information along with
its branches. The root node of the above
tree is A.
Ex:
Degree of a Node:
The no. of sub-trees of a node is called
degree of node. In otherwords, the no.
of children of a node is called degree.
In the above figure, degree of A is 3,
Degree of B is 2, Degree of H is
1 and degree of K is 0.
Terminal Nodes and Non-Terminal Nodes :
If the degree of node is zero, then
it is called terminal node or leaf node.
if the degree of node is not equal to zero then it is called
non-terminal node. In the above figure,
terminal nodes are J, F, L, K. The
remaining nodes are non-terminal nodes.
Parent and Children
If there is a branch(edge)from U to
V then U is called parent of V and V is called child of U. In the above tree, A’s children are
B,C,D. B’s childrens are E, F. I child is j etc., Parent of G is C, parent
of K is G etc.,
Siblings
Children
of the same parent are said to be siblings or brothers or sisters. In the above tree B, C, D are siblings, E, F
are siblings but G and H are cusions but not siblings.
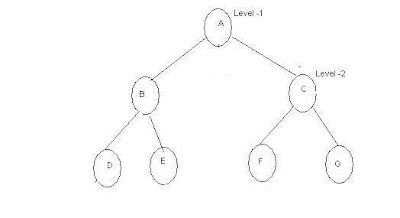
Level of a Node
Level of a node is defined as
distance of a node from root node +1. In
the above tree, the node at level one is A, nodes at level-2 are B,C,D, nodes
at level B are E,F,H,G.
Height of the tree
Height
of the tree is defined as largest level number in the tree. The height of above tree is 5. Since the largest level number is 5, where
node J is present.
Degree of a Tree
It is defined as maximum degree of
the nodes in the tree. The degree of the
above tree is 3. since maximum degree is
3 for node A.
Binary tree
A Binary tree is a tree, where each
should have maximum of two children i.e., degree of each node is less than or
equal to 2.
A binary tree of
zero node is said to be empty tree.
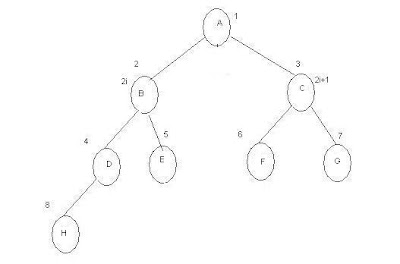
Complete Binary Tree
A
binary tree with n – nodes is said to be complete if and only if the no. of
nodes ranging from 1 to n. if the no. of
nodes i, then left child no. is 2i and right child number is 2i+1.
Ex
Invalid Node
Example
A
Binary tree is said to be full binary tree if each level contain 2i-1 nodes where
i is level no. i.e., level 1 should contain 20 nodes, level 2 contains 21 nodes, level 3 contain 22 nodes and so on.
Invalid Example
Every full binary
tree is a complete binary tree but the reverse is not true.



No comments:
Post a Comment