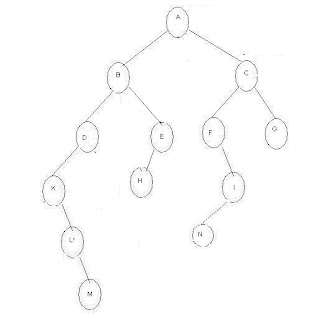
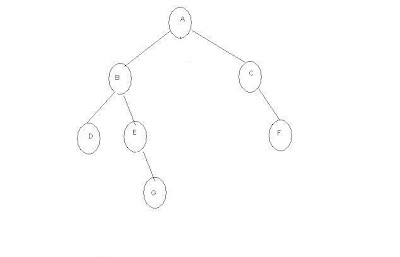
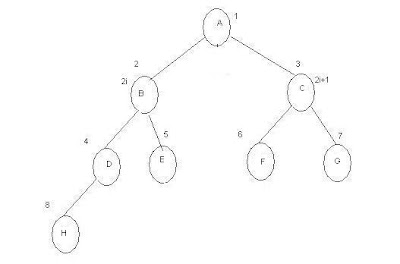
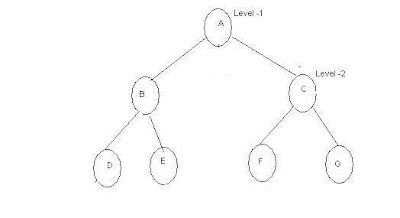
C Program to create
Tree using Menus
#include<stdio.h>
#include<math.h>
#include<conio.h>
#define MAX 100
struct node
{
struct node
*lchild;
char data;
struct node
*rchild;
};
struct node *s[MAX];
int top,top1,st[MAX];
void push1(int p)
{
if (top1==MAX-1)
printf("Stack is Full\n");
else
{
top1++;
st[top1]=p;
}
}
int pop1()
{
int p;
if (top1<0)
printf("Stack is Empty\n");
else
{
p=st[top1];
top1--;
}
return p;
}
void push(struct node *p)
{
if (top==MAX-1)
printf("Stack is Full\n");
else
{
top++;
s[top]=p;
}
}
struct node * pop()
{
struct node *p;
if (top<0)
printf("Stack is Empty\n");
else
{
p=s[top];
top--;
}
return p;
}
void displaytree(struct node *root)
{
int x,y,h,k;
struct node *p;
x=40;y=5;top1=0;h=0;top=0;
p=root;
s[top]=NULL;
while(p!=NULL)
{
gotoxy(x,y);
printf("%c", p->data);
if
(p->rchild!=NULL)
{
push(p->rchild);
k=x+ceil(40.0/exp((h+1)*log(2)));
push1(k);
k=y+3;
push1(k);
push1(h+1);
}
if
(p->lchild!=NULL)
{
p=p->lchild;
h++;
x=x-ceil(40.0/exp((h)*log(2)));
y=y+3;
gotoxy(x,y);
}
else
{
p=pop();
if (top1!=0)
{
h=pop1();
y=pop1();
x=pop1();
gotoxy(x,y);
}
}
}
}
struct node * getnode()
{
struct node *p;
p= (struct node *)
malloc(sizeof(struct node));
printf("Enter
data into a new node\n");
fflush(stdin);
scanf("%c",&p->data);
p->lchild=NULL;
p->rchild=NULL;
return p;
}
struct node * createtree()
{
struct node
*root,*p,*t;
char ch=0;
top=0;
s[top]=NULL;
root=getnode();
p=root;
while(p!=NULL)
{
printf("Is
the right child is existing for %c :
",p->data);
fflush(stdin);
ch=getchar();
if ((ch=='Y')
||(ch=='y'))
{
t=getnode();
p->rchild=t;
push(t);
}
printf("Is
the left child is existing for %c :
",p->data);
fflush(stdin);
ch=getchar();
if ((ch=='Y') ||
(ch=='y'))
{
t=getnode();
p->lchild=t;
p=t;
}
else
{
p=pop();
}
}
return root;
}
void rpreorder(struct node *p)
{
if (p!=NULL)
{
printf("%c
",p->data);
rpreorder(p->lchild);
rpreorder(p->rchild);
}
}
void rinorder(struct node *p)
{
if (p!=NULL)
{
rinorder(p->lchild);
printf("%c
",p->data);
rinorder(p->rchild);
}
}
void rpostorder(struct node *p)
{
if (p!=NULL)
{
rpostorder(p->lchild);
rpostorder(p->rchild);
printf("%c
",p->data);
}
}
void ipreorder(struct node *root)
{
struct node *p;
top=0;
s[top]=NULL;
p=root;
while(p!=NULL)
{
if(p->rchild!=NULL)
push(p->rchild);
printf("%c
", p->data);
if
(p->lchild!=NULL)
p=p->lchild;
else
p=pop();
}
}
void iinorder(struct node *root)
{
struct node *p;
top=0;
s[top]=NULL;
p=root;
while(p->lchild!=NULL)
{
push(p);
p=p->lchild;
}
while(p!=NULL)
{
printf("%c
", p->data);
if
(p->rchild!=NULL)
{
p=p->rchild;
while(p->lchild!=NULL)
{
push(p);
p=p->lchild;
}
}
else
{
p=pop();
}
}
}
void ipostorder(struct node *root)
{
struct node
*p,*temp;
top=0;
s[top]=NULL;
p=root;
temp=NULL;
while(p->lchild!=NULL)
{
push(p);
p=p->lchild;
}
while(p!=NULL)
{
if
((p->rchild==NULL)||(p->rchild==temp))
{
printf("%c
", p->data);
temp=p;
p=pop();
}
else
{
push(p);
p=p->rchild;
while(p->lchild!=NULL)
{
push(p);
p=p->lchild;
}
}
}
}
void menudisplay(int n)
{
int
i,row=10,col=30;
char
opt[9][20]={"Create Tree","Display Tree","Recursive
Preorder",
"Recursive
Inorder","Recursive Postorder",
"Iterative
Preorder","Iterative Inorder",
"Iterative
Postorder","Exit"};
clrscr();
textattr(177);
gotoxy(23,8);
cprintf("TREES Demonstration\n");
for
(i=0;i<9;i++)
{
if (i==n)
{
textattr(66);
gotoxy(col,row);
cprintf("%s\n",opt[i]);
row++;
}
else
{
textattr(7);
gotoxy(col,row);
cprintf("%s\n",opt[i]);
row++;
}
}
}
int selectoption()
{
char ch=0;
int curr=0;
menudisplay(curr);
while(ch!=13)
{
ch=getch();
textattr(7);
if (ch==27)
return 27;
if (ch==0)
ch=getch();
if (ch==72)
{
curr--;
if (curr<0) { curr=8; }
menudisplay(curr);
}
if (ch==80)
{
curr++;
if (curr==9) { curr=0; }
menudisplay(curr);
}
}
return curr;
}
void main()
{
int opt;
struct node *root;
clrscr();
while (1)
{
opt=selectoption();
if ((opt==27) ||(
opt==8)) { break; }
clrscr();
switch(opt)
{
case 0:{
root= createtree();
break; }
case 1:{
displaytree(root);
break; }
case 2:{
displaytree(root);
gotoxy(30,21);
printf("Preorder Traversal : ");
rpreorder(root);
break;
}
case 3:{
displaytree(root);
gotoxy(30,21);
printf("Inorder Traversal : ");
rinorder(root);
break;
}
case 4:{
displaytree(root);
gotoxy(30,21);
printf("Postorder Traversal : ");
rpostorder(root);
break;
}
case 5:{
displaytree(root);
gotoxy(30,21);
printf("Preorder Traversal : ");
ipreorder(root);
break;
}
case 6:{
displaytree(root);
gotoxy(30,21);
printf("Inorder Traversal : ");
iinorder(root);
break;
}
case 7:{
displaytree(root);
gotoxy(30,21);
printf("Postorder Traversal : ");
ipostorder(root);
break;
}
case 8:{
exit(0); }
}
gotoxy(30,22);
printf("Press any Key........\n");
getch();
}
textattr(177);
gotoxy(20,20);
cprintf(" Tree
Demonstration is Over. Press any
key....");
getch();
}